木易

# Road Map

# 单调栈

单调栈（单调队列）是一种维护栈内元素递增(或递减)的栈。

单调栈分为单调递增栈和单调递减栈，单调递增栈即栈内元素保持单调递增的栈，同理单调递减栈即栈内元素保持单调递减的栈。

单调栈里可以保存元素的值或下标

某些场景下，我们需要维护栈底，这时候栈的数据结构是不满足要求的，可能需要借助队列或双端队列实现（比如求滑动窗口最大值），即单调队列

# 应用场景

  • 可以在O(N)的时间复杂度，找出每个数左右两边第一个大于或小于它的解
  • 单调递增栈用于查找两边第一个小于当前元素的值，单调递减栈用于查找两边第一个大于当前元素的值
  • 一般数组中的单调性问题，题目中隐含第一个或离此元素最近的大于或小于元素的值，这类问题都可以考虑下，用单调栈是否可以求解

# 动画演示

数列7 4 9 5 3 2构建单调递减栈

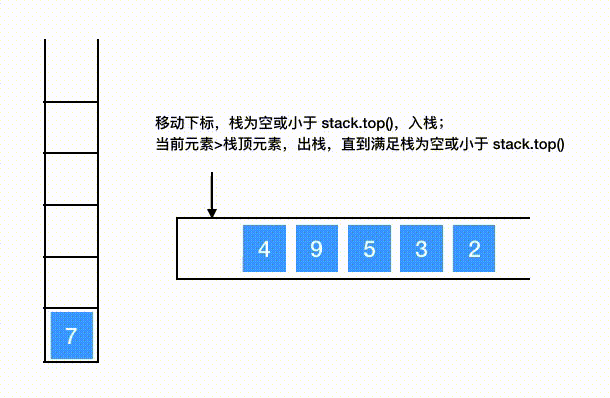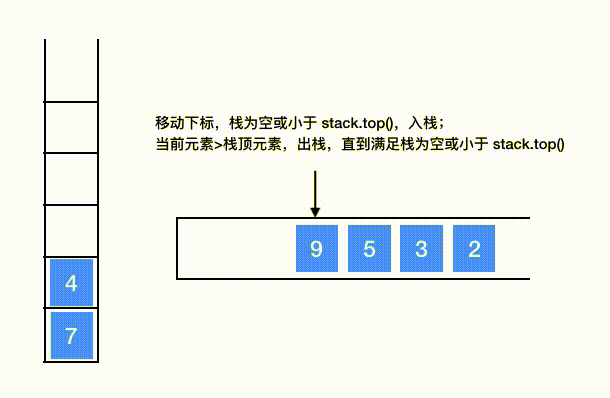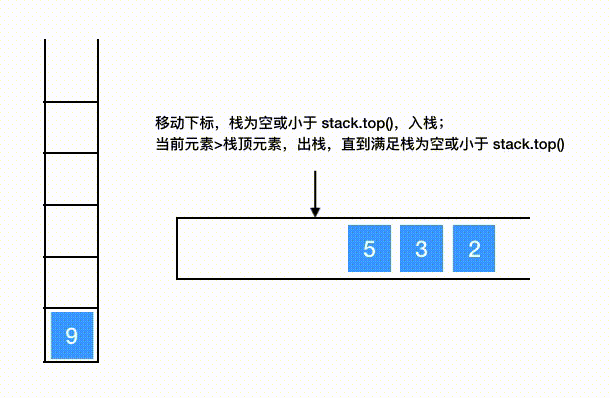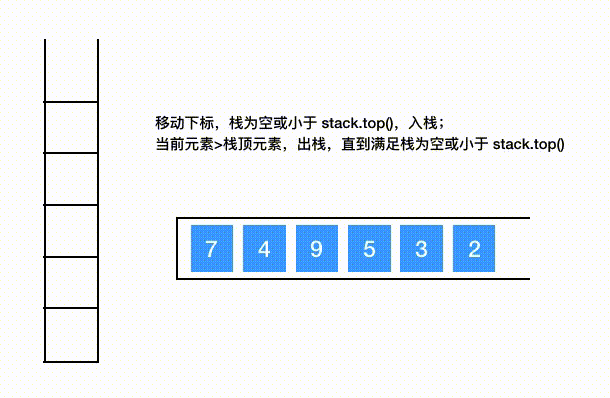
单调栈动画演示

# 代码模板

stack<int> stk;
for (int i = 0; i < A.size(); i++) {
    while (stk.size() && A[i] <= A[stk.top()]) { // 单调递增栈
        // 单调递减栈A[i] >= A[stk.top()]
        stk.pop();
    }
    stk.push(i);
}
1
2
3
4
5
6
7
8

# 模板题

给定一个长度为 N 的正整数数组，输出每个数左右两边第一个比它小的数，如果不存在则输出-1。

输入: [3, 4, 2, 7, 5]
输出：
左边：[-1, 3, -1, 2, 2]
右边：[2, 2, -1, 5, -1]
1
2
3
4

# 解题思路

查找左右两边第一个更小的元素，使用单调递增栈

  • 入栈时，当前元素左边的第一个更小的元素是当前栈顶元素
  • 出栈时，栈顶右边第一个更小的元素是即将入栈的当前元素

# 代码实现

void sumSubarrayMins(vector<int> &A) {
    int n = A.size();
    vector<int> lmin(n, -1); // 左边第一个更小的元素
    vector<int> rmin(n, -1); // 右边第一个更小的元素
    stack<int> stk; // 单调递增栈
    for (int i = 0; i < A.size(); i++) {
        while (stk.size() && A[i] <= A[stk.top()]) {
            rmin[stk.top()] = A[i];
            stk.pop();
        }
        if (stk.size()) lmin[i] = A[stk.top()];
        stk.push(i);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
public void sumSubarrayMins(int[] nums) {
    int n = nums.length;

    int[] lmin = new int[n];
    int[] rmin = new int[n];
    Arrays.fill(lmin, -1);
    Arrays.fill(rmin, -1);
    Deque<Integer> stk = new ArrayDeque<>();
    for (int i = 0; i < n; i++) {
        while (!stk.isEmpty() && nums[i] <= nums[stk.getLast()]) {
            rmin[stk.getLast()] = nums[i];
            stk.pollLast();
        }
        if (!stk.isEmpty()) lmin[i] = nums[stk.getLast()];
        stk.addLast(i);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

时间复杂度O(N)，空间复杂度O(N)

# 单调队列

← 0x43_并查集 →