# Road Map

# 树状数组

# 背景

区间求和可以使用前缀和去解，时间复杂度 $O(1)$ ；

但是如果元素可变呢？如何才能高效的维护前缀和数组，这时候就需要引入树状数组；

树状数组适用于带更新操作的区间和查询

# 原理

若一个正整数 $x$ 的二进制表示为 $a_{k-1}a_{k-2}...a_2a_1a_0$ , 其中等于 1 的位是 $\{a_{i_1}, a_{i_2}, ... , a_{i_m}\}$ ，则正整数 $x$ 可以二进制分解成：

$x = 2^{i_1} + 2^{i_2} + ... + 2^{i_m}$

不妨设 $i_1 > i_2 > ... > i_m$ , 进一步的，区间 $[1,x]$ 可以分成 $O(logx)$ 个小区间：

长度为 $2^{i_1}$ 的小区间 $[1, 2^{i_1}]$
长度为 $2^{i_2}$ 的小区间 $[2^{i_1} + 1, 2^{i_1} + 2^{i_2}]$
长度为 $2^{i_3}$ 的小区间 $[2^{i_1} + 2^{i_2} + 1, 2^{i_1} + 2^{i_2} + 2^{i_3}]$
...
长度为 $2^{i_m}$ 的小区间 $[2^{i_1} + 2^{i_2}+... + 2^{i_{m-1}} + 1, 2^{i_1} + 2^{i_2} +...+ 2^{i_m}]$

# 概念

树状数组(Binary Indexed Tree) ，也叫Fenwick 树、二叉索引树(Binary Indexed Tree)；

定义： $c[x]$ 保存序列 $a$ 的区间 $[x - lowbit(x) + 1, x]$ 中所有数的和，即 $\sum^x_{i=x-lowbit(x)+1} a[i]$

# 性质

每个内部节点 $c[x]$ 保存以它为根的子树中所有叶节点的和; 所有叶节点对应区间 $[x - lowbit(x) + 1, x]$
每个内部节点 $c[x]$ 的子节点个数等于 $lowbit(x)$ 的位数
除了根节点，每个内部节点 $c[x]$ 的父节点是 $c[x+lowbit(x)]$
树的深度是 $O(logn)$

# 解决问题

快速求前缀和
修改某一个数
每一个操作的复杂度都是 $O(logn)$

# 结构

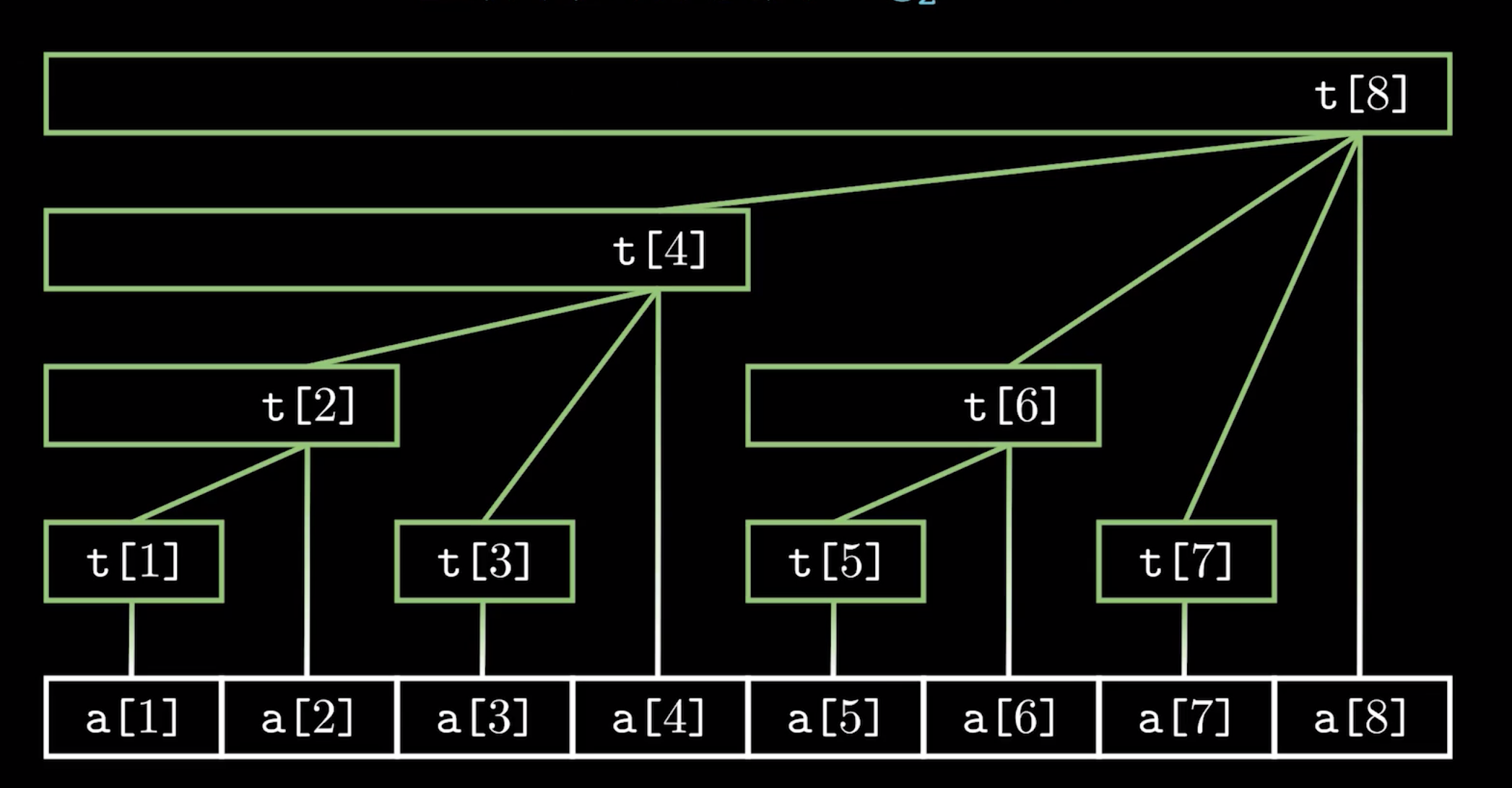
# 代码实现

# 单点修改，区间查询

基础版本

由 A 数组建立 C 数组

int n = A.size();
vector<int> C(n+1, 0);
for (int i = 1; i<=n; i++) {
    add(i, A[i-1]);
}

1
2
3
4
5

单点修改

void add(int x, int k){
    for (;x <= n; x += x&-x) t[x] += k;
}

1
2
3

区间查询[1,x],位置 0 为空

int ask(int x) {
    int ans = 0;
    for (; x >0; x-=x&-x) ans +=t[x];
    return ans;
}

1
2
3
4
5

单点修改：add(x, k);
区间查询：ask(r) - ask(l - 1);

# 完整版代码

class Solution {
public:
    vector<int> t;
    int n;

    void build(vector<int> &nums) { // 建树
        n = nums.size();
        t = vector<int>(n + 1, 0);
        for (int i = 1; i <= n; i++) {
            add(i, nums[i - 1]);
        }
    }

    void add(int x, int k) { // 修改某个点
        for (; x <= n; x += x & -x) t[x] += k;
    }

    int ask(int x) { // 查询区间[0,x]
        int ans = 0;
        for (; x>0; x -= x & -x) ans += t[x];
        return ans;
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

树状数组时间复杂度

预处理： $O(nlog n)$
更新和查询： $O(log n)$

# 区间修改，单点查询

使用差分，维护差分数组d[i] = a[i] - a[i - 1]。区间更新变成了[l, r] 两端 l 和 r 的更新，点查询也就变成了[1, x]的区间更新。

# 区间修改，区间查询

使用差分，维护差分数组 d1[i] = a[i] - a[i - 1] 和 d2[i] = i _ (d2[i] - d2[i - 1])。区间更新的方式和 2 相同，区间查询是(r + 1) _ query(d1, r) - query(d2, r)。通过差分推一推就能得到。 当遇到单点更新时，树状数组往往比线段树更实用

# 树状数组和线段树比较

树状数组功能比线段树少，实现简单，常数小
树状数组通常只能用于区间求和
线段树能够应用于更多场景，包括：处理区间最大值/最小值等一系列问题
线段树实现较复杂，代码长一些

← 0x46_二叉搜索树 0x48_线段树 →