# Road Map

# 状态压缩 dp

状态压缩 dp，用整数来描述一个集合从而达到节省时间空间，让代码更加的好写

整数的二进制表示状态，通过位运算进行状态转换

# 旅行商问题

旅行商问题（Traveling Salesman Problem）,简称 $TSP$ 问题

问题描述：

n 个点，m 条边，找出最短的回路

题目练习:

旅行商问题 (opens new window)

# 算法 1

# 暴力枚举

假设有 1，2，3，4，5 五个点

枚举所有排列：

1 —> 2 -> 3 -> 4 -> 5
1 —> 2 -> 3 -> 5 -> 4
1 —> 2 -> 4 -> 3 -> 5
1 —> 2 -> 4 -> 5 -> 3
...
5 —> 4 -> 3 -> 2 -> 1

1
2
3
4
5
6

# 时间复杂度

$O(n!)$

# 算法 2

# 状态压缩 DP

枚举所有排列存在重复计算的问题

集合用 S 表示， $dp[S][i]$ 表示走过了 S 集合，到达位置 i 的最小代价

比如: 集合 $U(1,3,4)$ 停留在位置 3， $S=01101$ 表示集合 $U(1,3,4),$ 状态表示为 $dp[01101][3]$

状态转换：

$i->j$ 的转换过程： $dp[S|1<<j][i] = min(dp[S][i]+(i,j), dp[S|1<<j][i])$

# 时间复杂度

$O(2^n)$

# 代码实现

#include <bits/stdc++.h>
using namespace std;

const int N = (1 << 16) + 10;
int n, m; // n 个点，m条边
int dp[N][16];
int dis[16][16];
int main() {
    cin >> n >> m;
    while (m--) {
        int u, v, w;
        cin >> u >> v >> w;
        dis[u][v] = w;
        dis[v][u] = w;
    }
    memset(dp, 0, sizeof dp);
    memset(dis, 0x3f, sizeof dis);
    int M = (1 << n) - 1;
    for (int i = 0; i < n; i++)
        for (int j = 0; j <= M; j++)
            dp[i][j] = 1e9;
    dp[0][1] = 0;
    for (int s = 1; s < M; s++) // 枚举所有状态
        for (int i = 0; i < n; ++i) // 枚举n个城市
            for (int j = 0; j < n; ++j) // i -> j
                if (!(s >> j & 1)) { // 如果当前城市j还没有经过,我们从i走向j
                    int next = s | (1 << j);
                    if (next == M)
                        dp[j][next] = min(dp[j][next], dp[i][s] + dis[i][j] + dis[j][0]);
                    else
                        dp[j][next] = min(dp[j][next], dp[i][s] + dis[i][j]);
                }
    int ans = 1e9;
    for (int i = 1; i < n; i++)
        ans = min(ans, dp[i][M]);
    cout << ans << endl;
    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

# P 和 NP

P 问题(Polynomial): 时间复杂度都可以用 $O(N^K)$ 来表示，k 是一个常数，多项式时间算法
NP 问题(Non-deterministic Polynomial): 意思是“不确定是否能用多项式时间解决”，时间复杂度： $O(2^N)$ ，甚至 $O(N!)$ , 这些时间复杂度随着问题规模 N 的增长，计算量的增长速度是非常恐怖的 NP = P？

有些科学家认为，所有的 NP 问题终究都可以在多项式时间内解决，只是我们暂时还没有找到方法；也有些科学家认为，某些 NP 问题永远无法在多项式时间内解决。这个业界争论可以用一个公式来表达：NP = P？

# 归约和 NPC

归约的定义：只要有办法解决 Q'，就一定能够解决 Q，则称：问题 Q 归约于问题 Q'

归约可以逐级传递，比如问题 A 归约于问题 B，问题 B 归约于问题 C，问题 C 归约于问题 D，那么我们可以说问题 A 归约于问题 D

NPC 问题（NP-complete）：存在归约关系的 NP 问题，可以用归约的方式求解

就数量上而言，NP 问题远比 P 问题要多，而 NP 之中的 NPC 问题也仅占极少数，所以 P、NP、NPC 之间的关系可以用下图来表示：

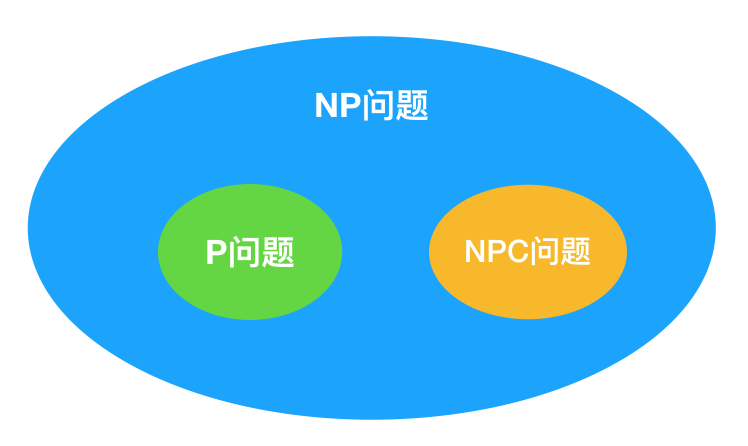
np-p-npc

旅行商问题就是一个NPC问题

# 题目

# #2153. 「SCOI2005」互不侵犯 (opens new window)

状态压缩 OI-WIKI (opens new window)

import java.util.Map;
import java.util.Scanner;
import java.util.TreeMap;
public class Main {

    boolean check(int i, int j) {
        if ((i & (i << 1)) > 0)
            return false;

        if ((j & (j << 1)) > 0)
            return false;
        if ((i & j) > 0)
            return false;
        if (((i << 1) & j) > 0)
            return false;
        if (((i >> 1) & j) > 0)
            return false;
        return true;
    }
    public long kingCnt(int N, int K) {
        long f[][][] = new long[N + 1][1 << 9][K + 1];
        int[] cnt = new int[1 << 9]; // 枚举 各个状态的 国王数

        for (int i = 0; i < (1 << 9); i++) {
            cnt[i] = cnt[i >> 1] + (i & 1);
        }

        f[0][0][0] = 1;

        for (int i = 1; i <= N; i++) {
            for (int j = 0; j < (1 << N); j++) { // 当前行状态
                for (int t = 0; t < (1 << N); t++) { // 当前行的上一行状态
                    if (!check(t, j))
                        continue;

                    for (int k = cnt[j] + cnt[t]; k <= K; k++) { // 枚举 前j 行有多少个国王
                        f[i][j][k] += f[i - 1][t][k - cnt[j]];
                    }
                }
            }
        }
        long ans = 0;

        for (int i = 0; i < (1 << N); i++) {
            ans += f[N][i][K];
        }

        return ans;
    }
    public static void main(String[] args) {

        Scanner scanner = new Scanner(System.in);
        Main ccc = new Main();
        int N = scanner.nextInt(), K = scanner.nextInt();
        System.out.println(ccc.kingCnt(N, K));
    }

}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

# AcWing327.玉米田 (opens new window)

import java.util.Collections;
import java.util.Scanner;
import java.util.TreeMap;
public class Main {

    /**
     * 判断状态是否合法
     * S:田地
     * i:上一行
     * j: 本行
     * c: 本行的索引
     */
    boolean check(int[] s, int i, int j, int c) {
        if (c > 1 && (i & (i << 1)) > 0) return false; // 上一行 自己是否存在相邻
        if ((j & (j << 1)) > 0) return false;// 本行 自己是否存在相邻
        if (c> 1 & (i & j) > 0) return false; // 上一行 和本行是否 相邻
        if ((~s[c - 1] & j) > 0) return false; // 贫瘠地段过滤
        return true;
    }
    public long count(int[] S, int M, int N) {

        int MOD = 100000000;
        int[][] f = new int[M + 1][1 << N];
        f[0][0] = 1;
        for (int i = 1; i <= M; i++) {
            for (int j = 0; j < (1 << N); j++) {
                for (int t = 0; t < (1 << N); t++) {
                    if (!check(S, t, j, i)) continue;
                    f[i][j] += f[i - 1][t];
                }
            }
        }
        int ans = 0;
        for (int i = 0; i < (1 << N); i++) {
            ans = (ans + f[M][i]) % MOD;
        }
        return ans;
    }

    public static void main(String[] args) {

        Scanner scanner = new Scanner(System.in);
        Main ccc = new Main();
        int M = scanner.nextInt(), N = scanner.nextInt();

        int[] st = new int[M];
        for (int i = 0; i < M; i++) {
            for (int j = 0; j < N; j++) {
                st[i] = (st[i] << 1) + scanner.nextInt();
            }
        }
        System.out.println(ccc.count(st, M, N));
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

← 0x53_博弈论 0x55_树形dp →